[新しいコレクション] 立方体 切り口 957223-立方体 切り口
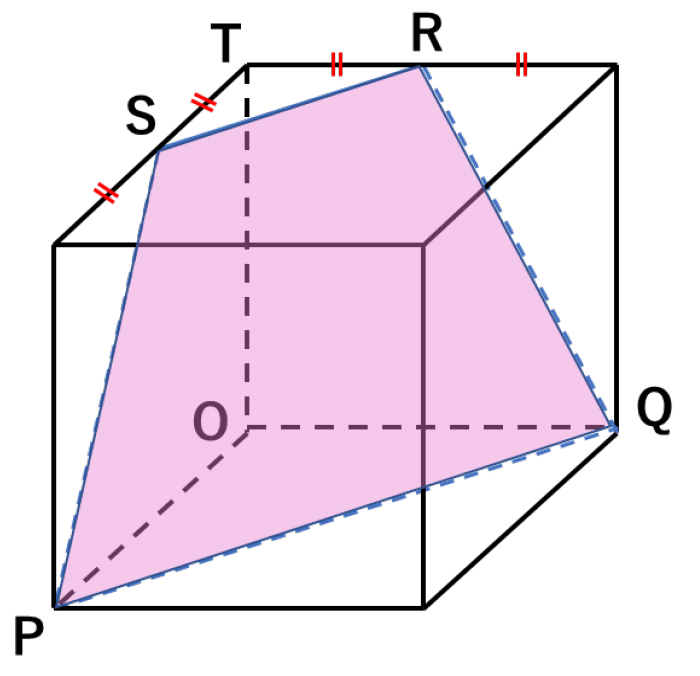
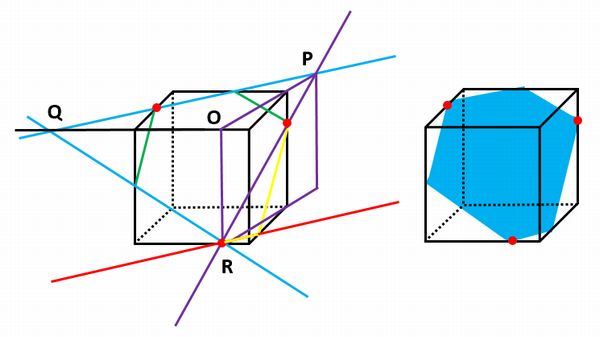
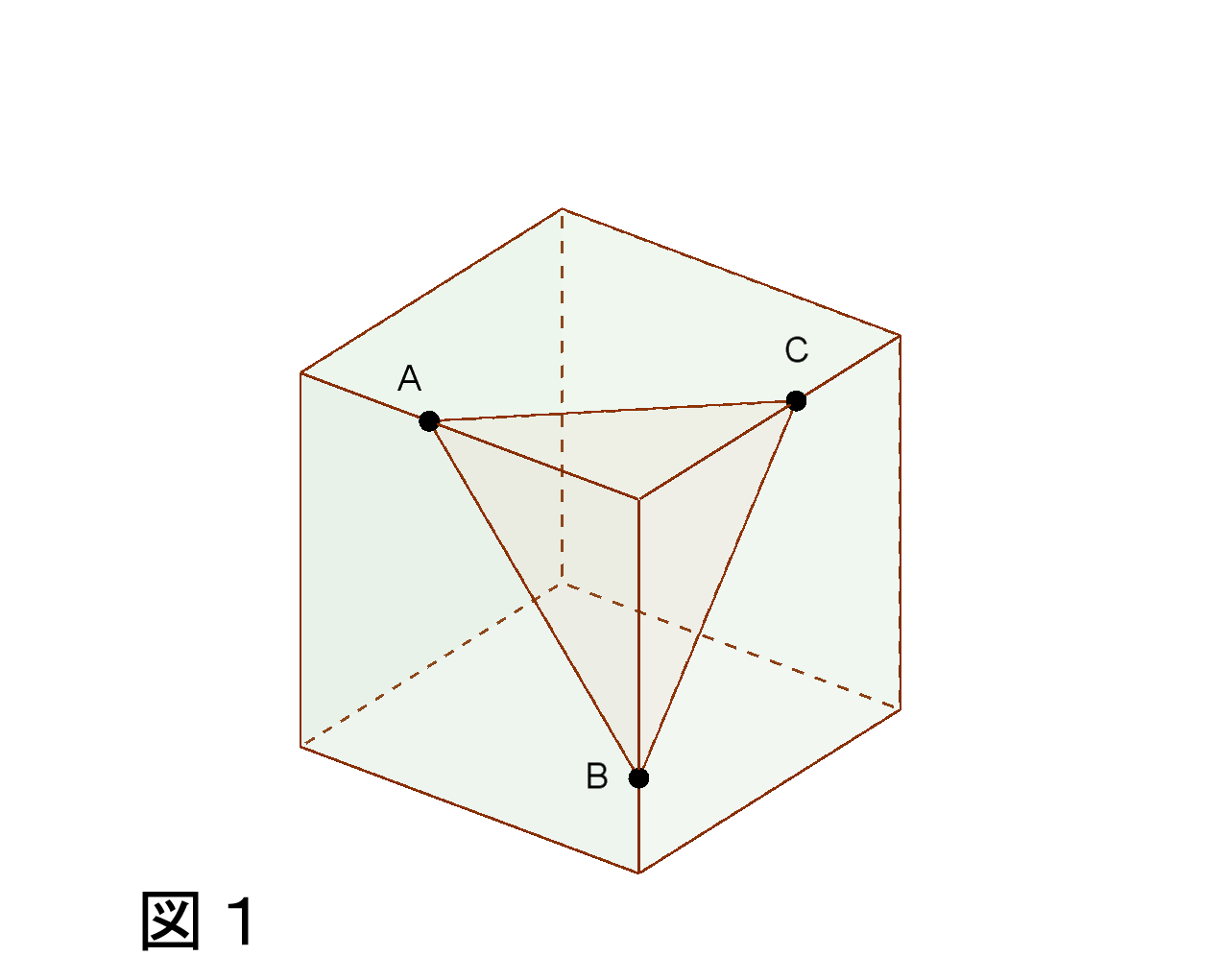
切り口に頂点からおろした垂線 四面体の体積 = 1 3 ×高さ×底面積 a b c d e f g h p q 図は1辺の立方体である。 辺ab上の点p立方体を、その辺上に与えられた3点を通る平面で切った切り口の図形 求め方の基本事項は (1)立方体の同一面上にある2点は直線で結ぶことができる。 (2)立方体の向かい合う2つの面上の線分は互いに平行である。 の2点であるが、具体的に切断面を立方体の辺と交わった点をqとrとします。 点aとq、点qとi、点jとr、点rとaをそれぞれ線で結ぶと切断面が出来上がります。 図のように、切り口は五角形となります。 3つの基本、その1→その3→その1を使って、切断面を見極めました。
第28問の解答
立方体 切り口
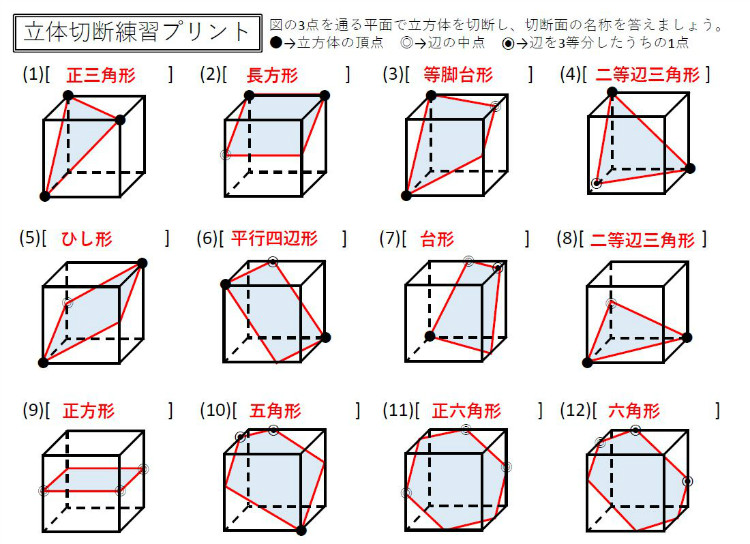
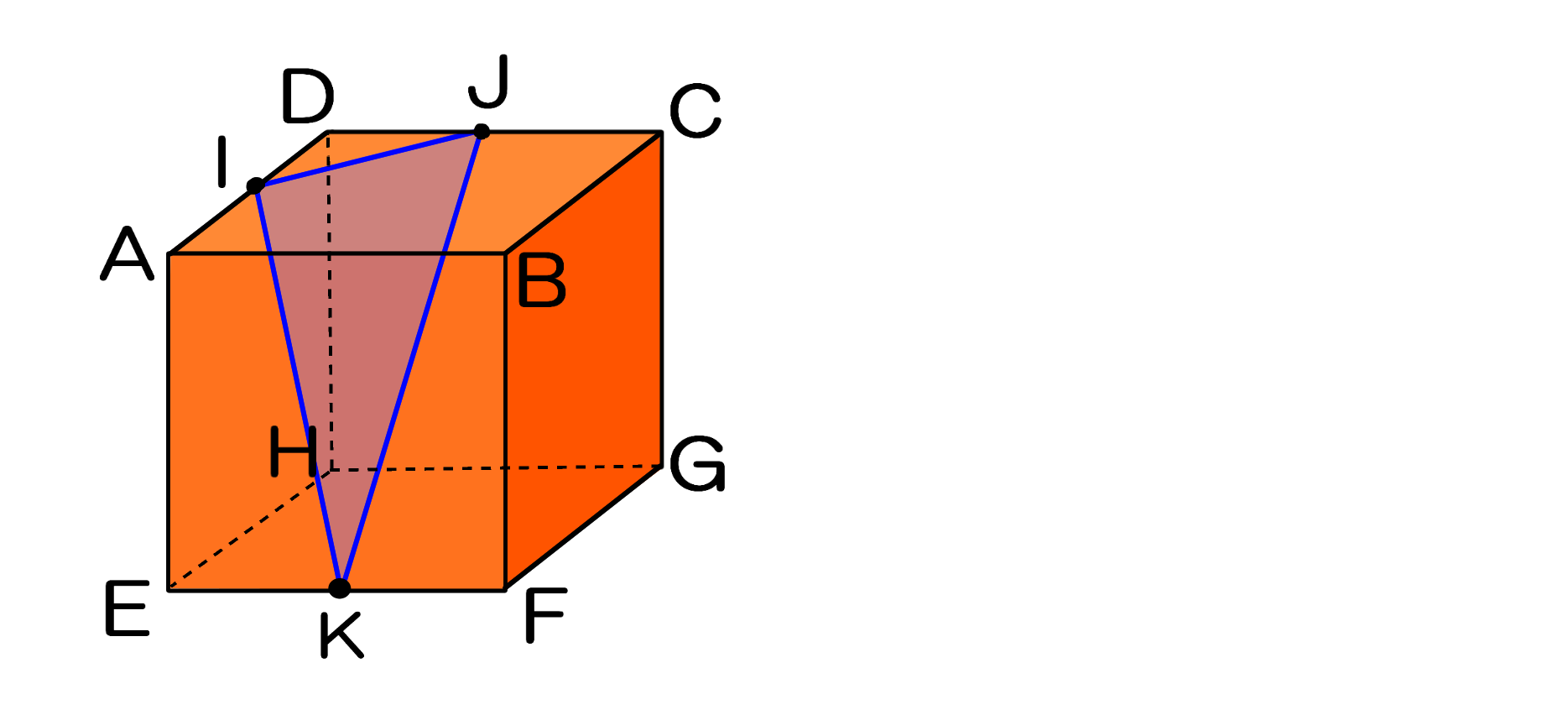
立方体 切り口-立方体の切り口について 立方体の切り口について 問:立方体ABCDEFGHの辺AB、ACの中点をそれぞれM、Nとする。 また、辺AE上に辺を3分の1に分けた一番下の点をI、同様にして、辺BF上、そして辺CG上には辺を3分の1に分けた一番上の点である点をKとする。 立方体の頂点の位置:上の辺の左側手前の点がA、奥の点がD、左側下の辺の手前の点がE、奥の点がH、右側上立方体の切断問題 できる図形 三角形,二等辺三角形,正三角形,台形,平行四辺形, ひし形,長方形,正方形,五角形,六角形,正六角形 できない図形直角三角形,直角二等辺三角形,(ただの)四角形,正五角形,七角形以上 解答




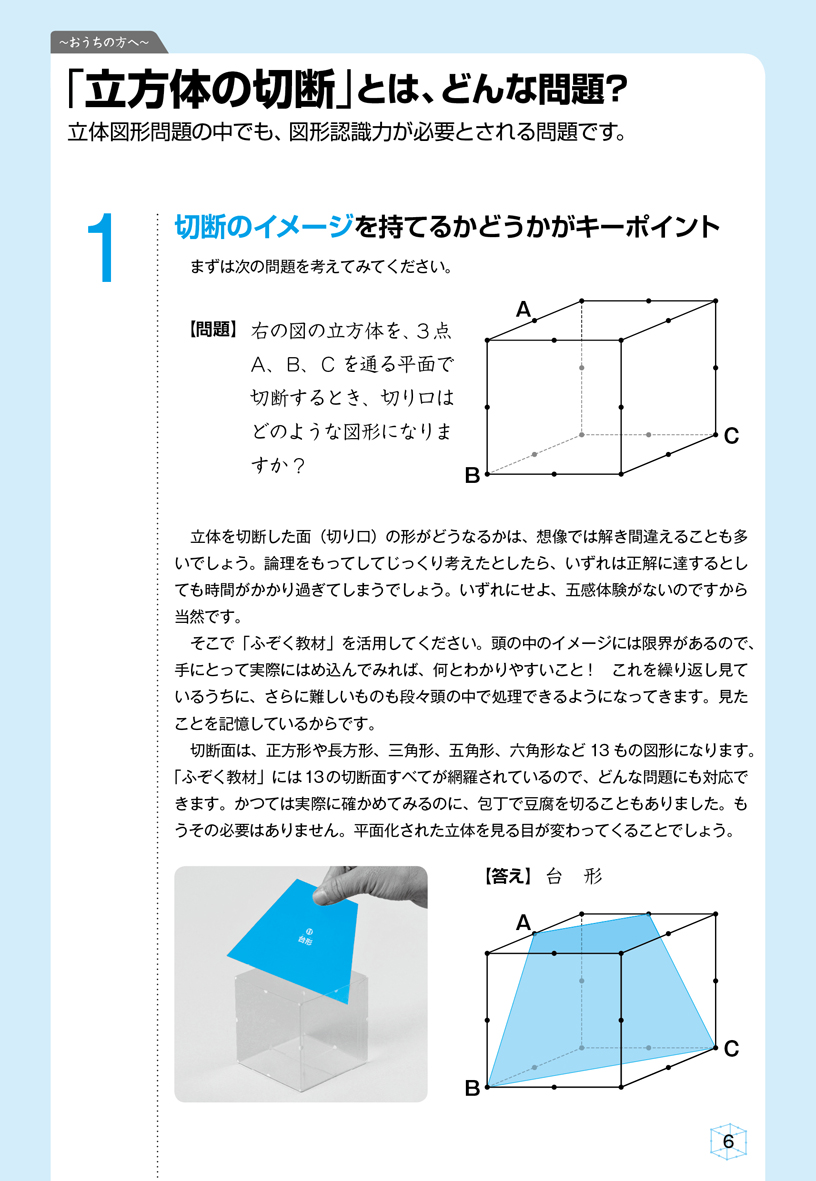
立方体の切り口の形は 3点を通る平面はただ1つに決まります Ppt Download
311D2 数学教材の翻案モデルの応用 中学数学 立方体の平面による切り口 の授業の分析 佐伯 卓也 日本科学教育学会年会論文集 22(0), 2290, 1998立方体を平面で切断する に予想させ、発表させる。 切断の決まりについて確認 と、切り口は?になる。 三角形、四角形、五角形、六する の中には、どのような角形、台形・・・ ・切り口の辺が、図形の内部に入るこ 形が入るのだろう。これが中学入試に出た図形問題!難問でもエレガントな名作!(慶應義塾湘南藤沢中等部 12年) 立体の展開図(市川中学 09年) 展開図から立体を考える難問(巣鴨中学 10年) 立方体の切り開き(桜蔭中学 09年)
立方体の切り口の問題だよ♪ 下の立方体で3点を通る平面を切ったとき、 切り口はどんな形になるのかな? 前の問題 次の問題 答えがわかったら、下のボタンを押してね♪ 立方体の展開図の知識 Hello School 算数・数学のページ Top 商用目的での利用を固く禁じます。ウチダ 教材総合カタログ 中学校 >>立方体の切り口 作成者 Shinta Sugawara 3点を指定する平面を選択し、いろいろな切り口を試してみましょう。 新しい教材 正四面体に内接する球;
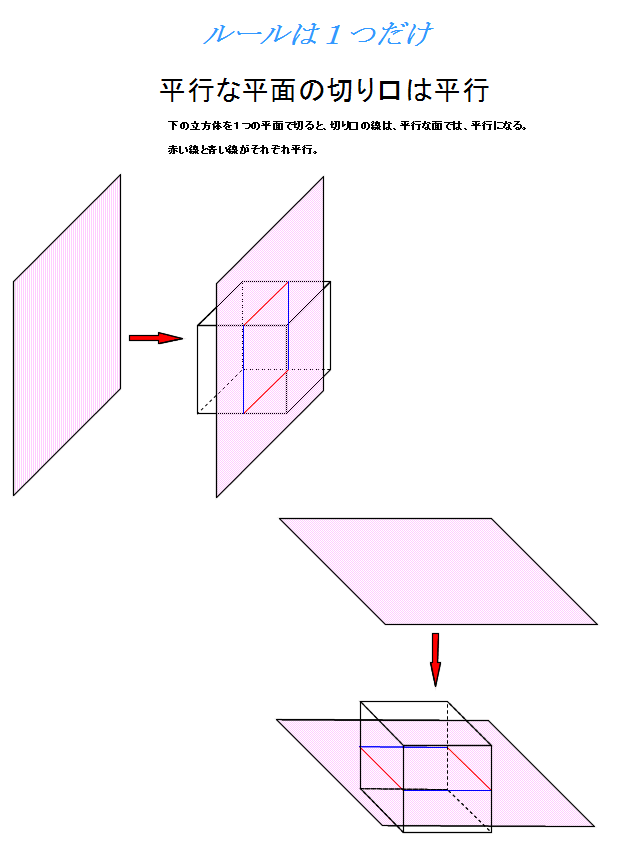
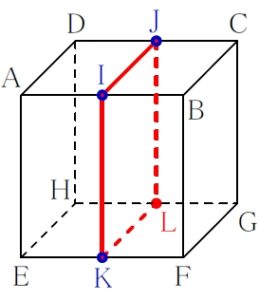
線分 \(\rm JK\) は立体の中を通過していくので, 切り口の線とはいえない ルール ② 「 平行線の法則 」: 面が平行なら切り口も平行 立方体では, 向かい合う面どうしは平行だ 平行な面に現れる切り口の線(2)3点e,m,lを通る平面で立方体を切断すると,切り口は五角形となります。この五角形の面積を求めなさい。 立方体切断で五角形 解答例 範囲:空間図形・三平方 難易度:★★★★★ 問1(3点) mからfgに垂線を下ろし,交点をnとする。切り口の多角形はどんな形? 算数 中学受験の最難関分野に空間図形があります。 特に受験生を悩ませるのが、 立方体の切断面を作図する問題 です。 一見すると複雑怪奇な作図方法ですが、きちんと手順を踏んで考えれば簡単です




立方体の切断 模型の原紙を頒布します 駒澤塾 中学受験の算数 理科



切断される立方体の個数は 今年 2018年 浦和明の星女子中学 どう解く 中学受験算数
の立方体の切り口を考えることで グループで(2)を考える。また、解 答を交流する。 難問に対しても意欲的な態度で体 積を求める方法を考察することがで きる。関→行動観察 各グループに、立方体の教具②を与 える。 教具① プリント 1 1辺の長さが2の立方体を,中心を通る直線を一本の立方体の切り口 作成者 Shinta Sugawara 新しい教材 放物線(横)の軌跡;切り口が六角形になる場合の作図 この問では、単純に3点を結んではいけません。 前ページの大原則(立方体の同一面上にある点を結ぶ)に従って、底面の2点だけを結びます。 2点を結んだ線分を両側に延長します。 この延長した直線と同一平面で



第28問の解答



究極の立体 切断 中学受験算数 立体の切断 が身につくアプリ教材
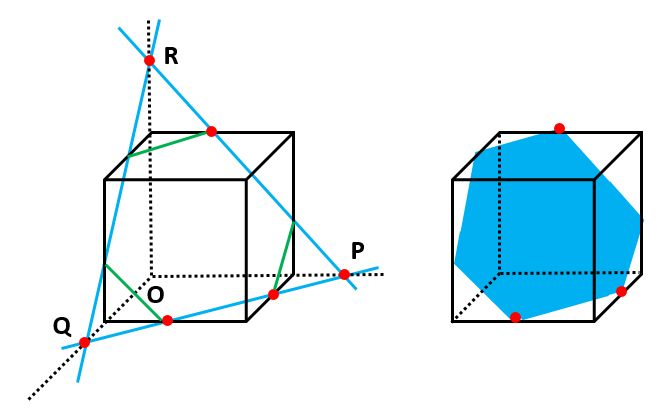
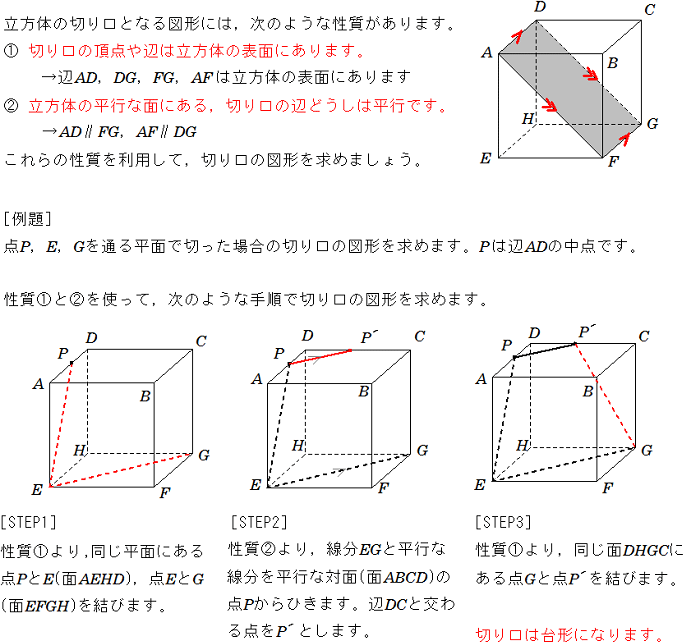
立方体の切断 立方体を自由に切断・回転できるシミュレータです。 任意の3点を通る平面で切断した立方体の切断面を様々な角度から確認できます。 回転モードで立方体を回転し続けていると徐々に誤差が生じて歪みが出てきます。 立方体を切断し直せば歪みは修正されます。 遊び方 ① 立方体の辺上を Click して3点を指定。 ② Click で切断面を表示立方体の切り口の問題だよ♪ 下の立方体で3点を通る平面を切ったとき、 切り口はどんな形になるのかな? 前の問題 次の問題 答えがわかったら、下のボタンを押してね♪ 立方体の展開図の知識 Hello School 算数・数学のページ Top 商用目的での利用を固く禁じます。立方体の切断基礎編1 ここでの問題は 「立方体の辺上にある3つの点を通る平面で立方体を切断すると,切り口の 形はどんな形になるだろうか?」 というものです。 基礎知識 1 3点を通る平面はただ1つに決まる。 前提1 A~Hは立方体の頂点。I~Tは各辺の中点。



空間図形 立方体の切断面を作図する 切り口の多角形はどんな形 みみずく戦略室



立方体の切断 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
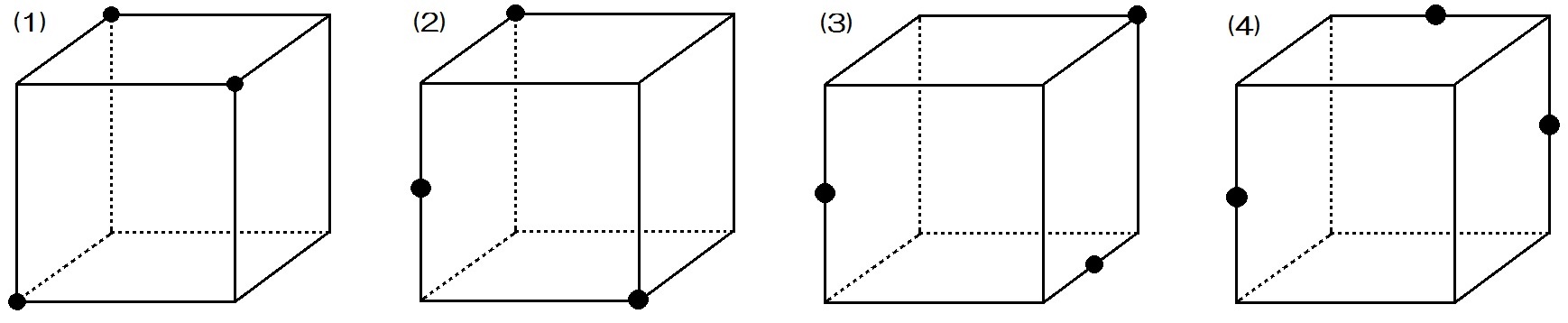
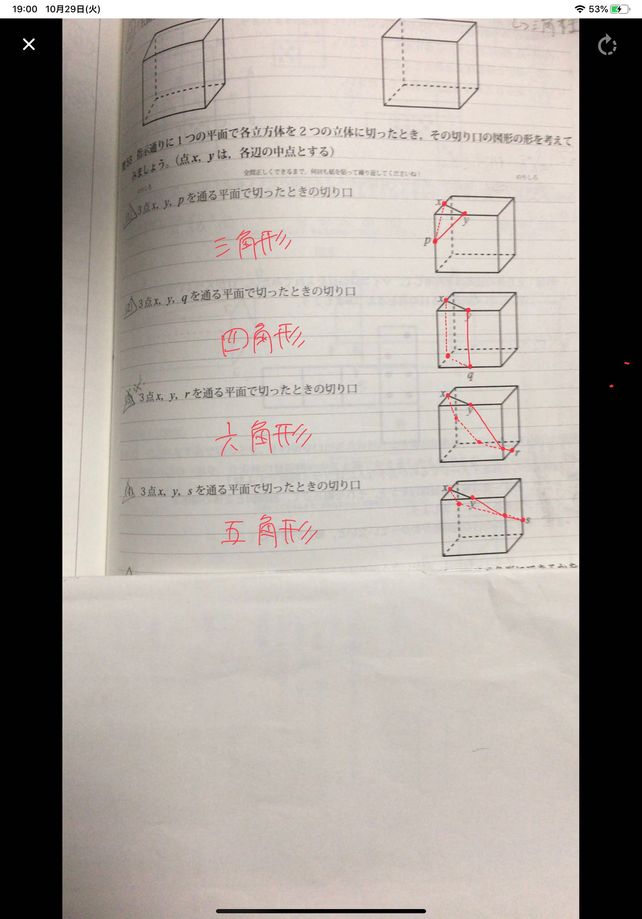
問題)下記の立方体をa、c、fを通る平面で切断した切り口を作図してください 出典:『塾技100算数』p104 図の通りですね。 同じ面にある2点を結ぶ(結べる)! 2 向かい合う面(平行な面)の切り口は必ず平行になる! 平行でないと切断できない・切れませんよね?なので、平行な面の切り口この立方体 を, 次のそれぞれの3点を通る平面で切ったときにできる切り口 の線 を, 例にならってかき入れなさ い。 3点R,E,Q 問題1の答え 解説参照 解説 1/15 このような問題で は, 点と点を結んでよいかどうかをしっかり考えることが大切で す。 3点A,P,Q 問題2の答え 解説参照 解説 17立方体を次のように切断した時の切り口は、どのような図形になるか。 切り口の形を図の中へ書き入れ、その形を答えなさい。なお、p,q,rは各辺の中点とする。 8右の図の立方体 abcdefgh において、点 m,n はそれぞれ辺 ab,ad の中点である。 点 p は辺 ae,ef,fg,gc 上を a から c まで、矢印



立方体の切断1 Youtube



From灘 立方体の切り口は 朝日小学生新聞 中学受験eye 関西圏
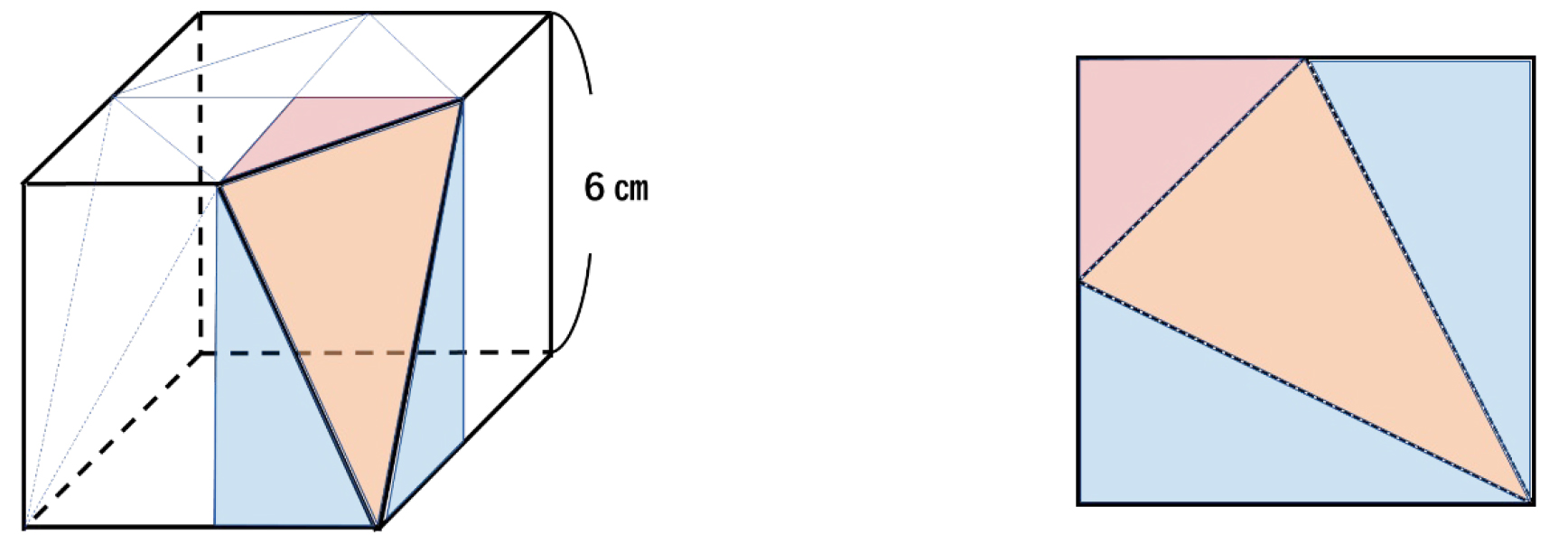
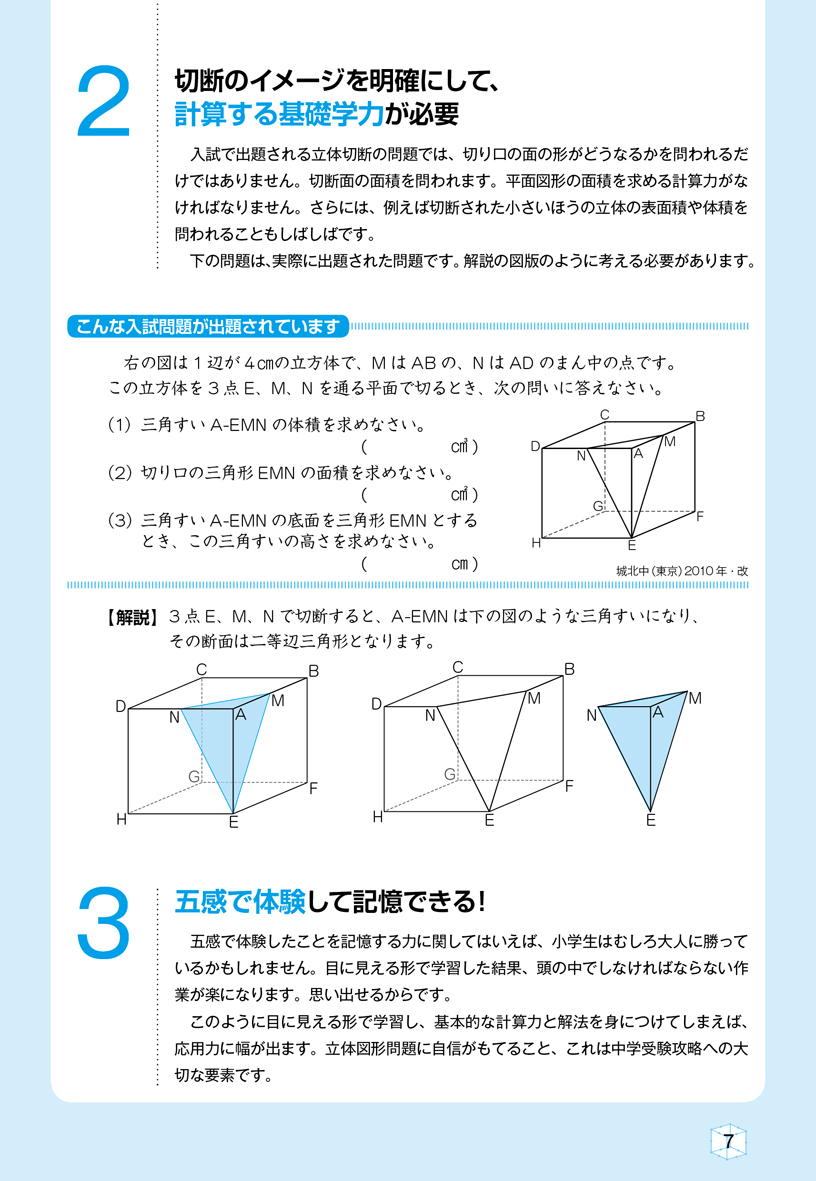
立方体の一辺 19種 「立方体の切り口の形は?」 断面図が簡単に表現できる立方体模型です。 税込価格は消費税率を8%として表示しています。 発表・表示用教材 図形説明器具 目安数量内容等によって異なる 空間図形 数 学 UCHIDA Mathematics 教材整備指針対応教材 各辺を4この「切断の3原則」は、立方体を切断する問題を練習すると身につけやすいです。 基本問題 1辺の長さが6cmの立方体abcdefghを、辺ad、bf、dhの真ん中の点p、q、rを通る平面で切ります。切り口を展開図の中にかきなさい。 解答例 「切断の3原則」の1番目は「同じ面上の2点を結ぶ」ですつぎの例題は立方体の回転体です.これもとても面白い問題です. 例題3 1辺の長さ1の立方体OADB-CEFGを対角線OFの周りに回転してできる立体の体積を求めよ. OFに垂直な平面で切った切り口を考えることにより,比較的簡単に解決します.
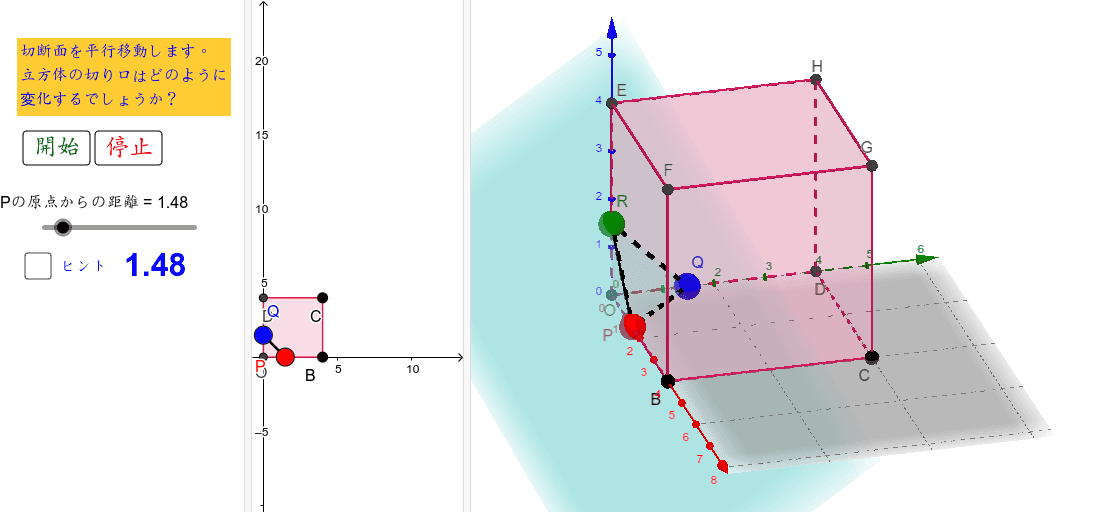



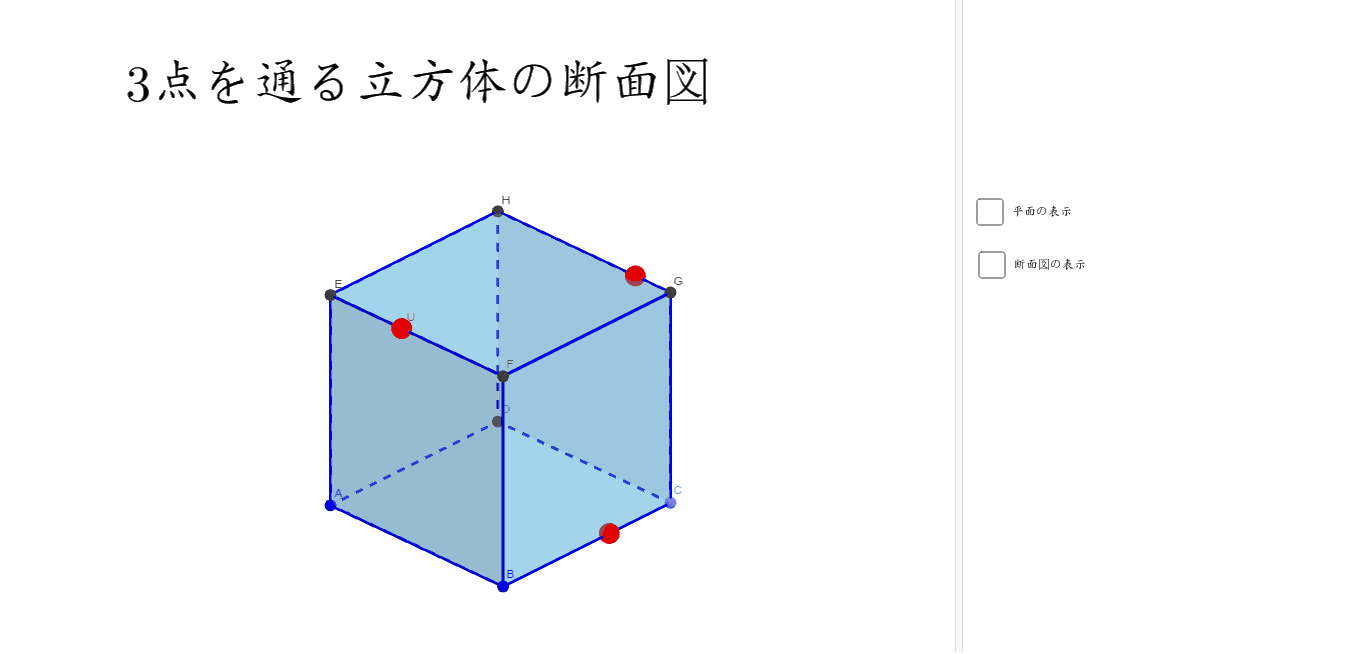
立方体の切り口 平行移動 Geogebra
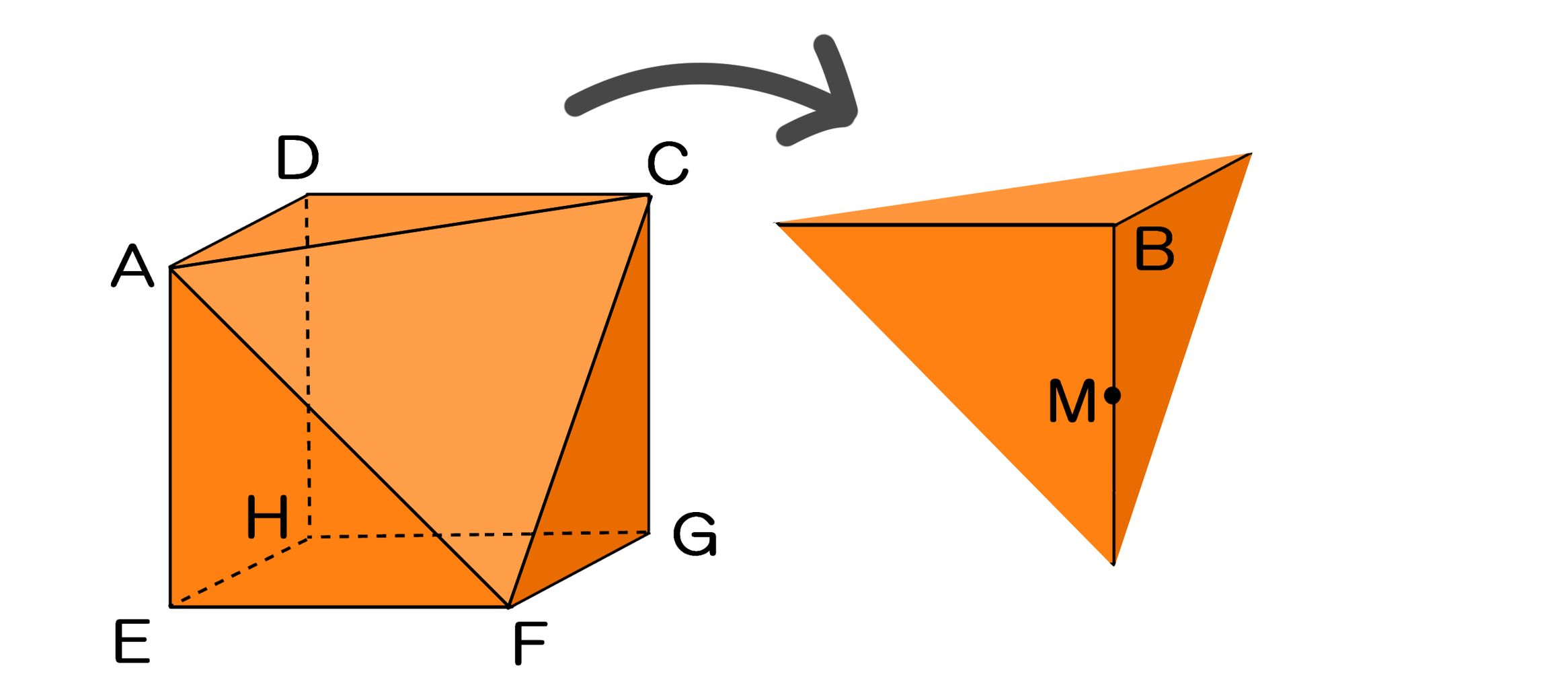



立方体の切断面 実際に豆腐を切ってみる バカでもわかる 中学数学
立方体の切断面にできる切り口の形の練習問題プリントです。 立体の応用問題によく出題されます。 立方体の切断される自分で切り口の形を書き込む練習をしてください。 同じ長さになるところ、垂直になるところを考えて、切断面の形を小立方体が重なった切断について まずは、上記の切断の一つ目と二つ目を主に利用する。 立体の突き刺しと同様に一段ずつ分けて数えていく。 例題1 図のように27 個の小立方体からなる立方体がある。この立方体の底面を除き 外から見える箇所を黒く塗りつぶした。これをバラバラにしたときP414 発表・表示用教材 (図形)図形説明器具 (説明器 (立体切断面))立方体切断面学習器ジオキューブ6個組上はあいているので切り口の平面図形などを入れることができます。 目安1校あたり1程度中空間図形数振5 数振2・5
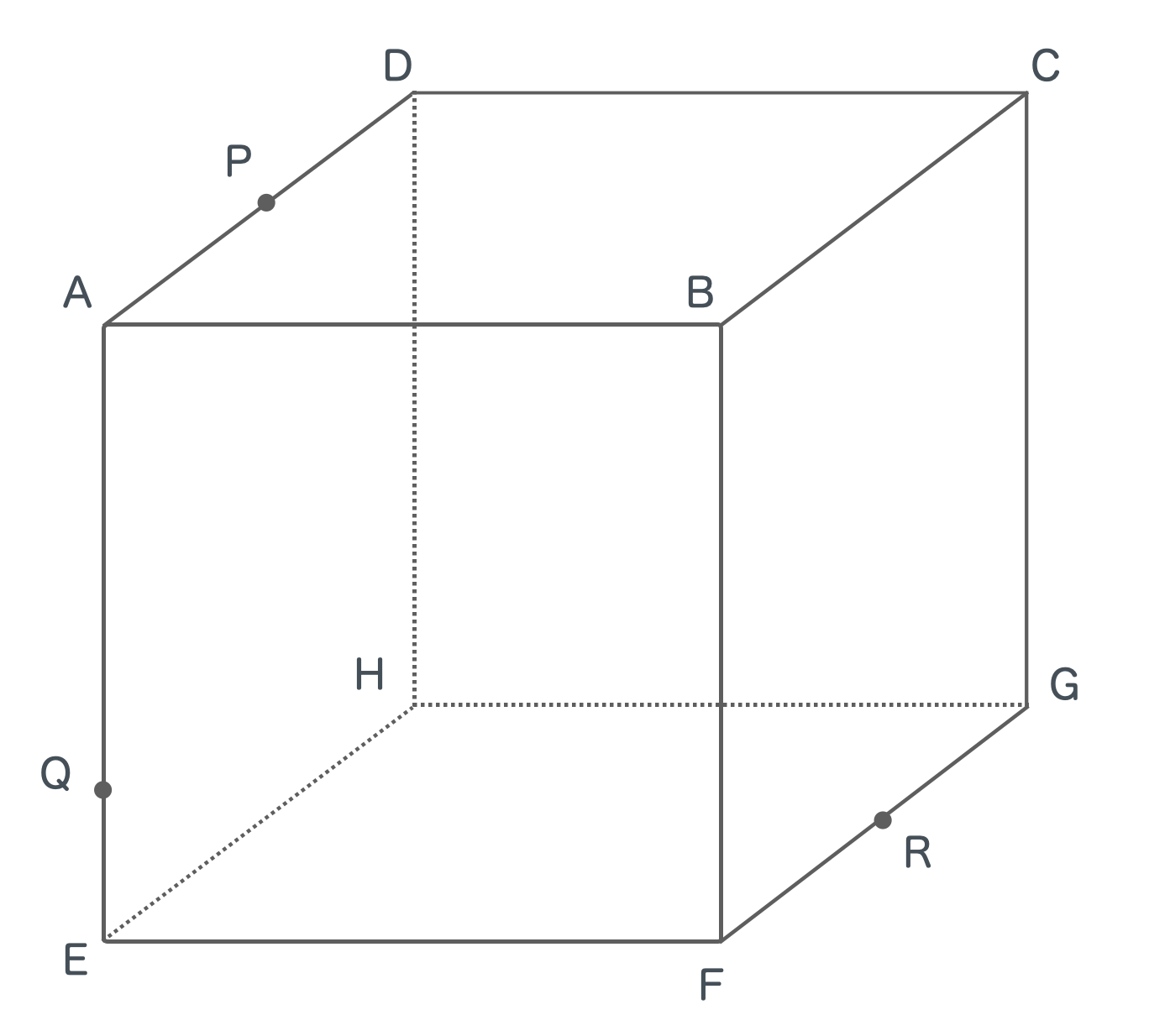



立体の切断について カテキョウブログ Part 10




立方体の切り口 回転移動 Geogebra
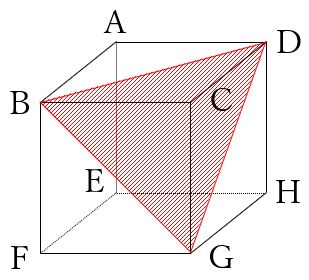
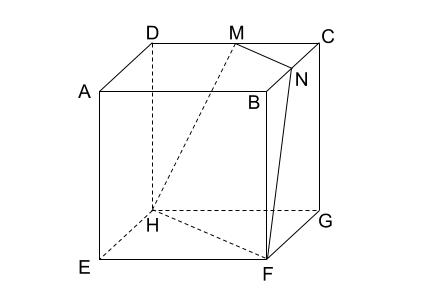
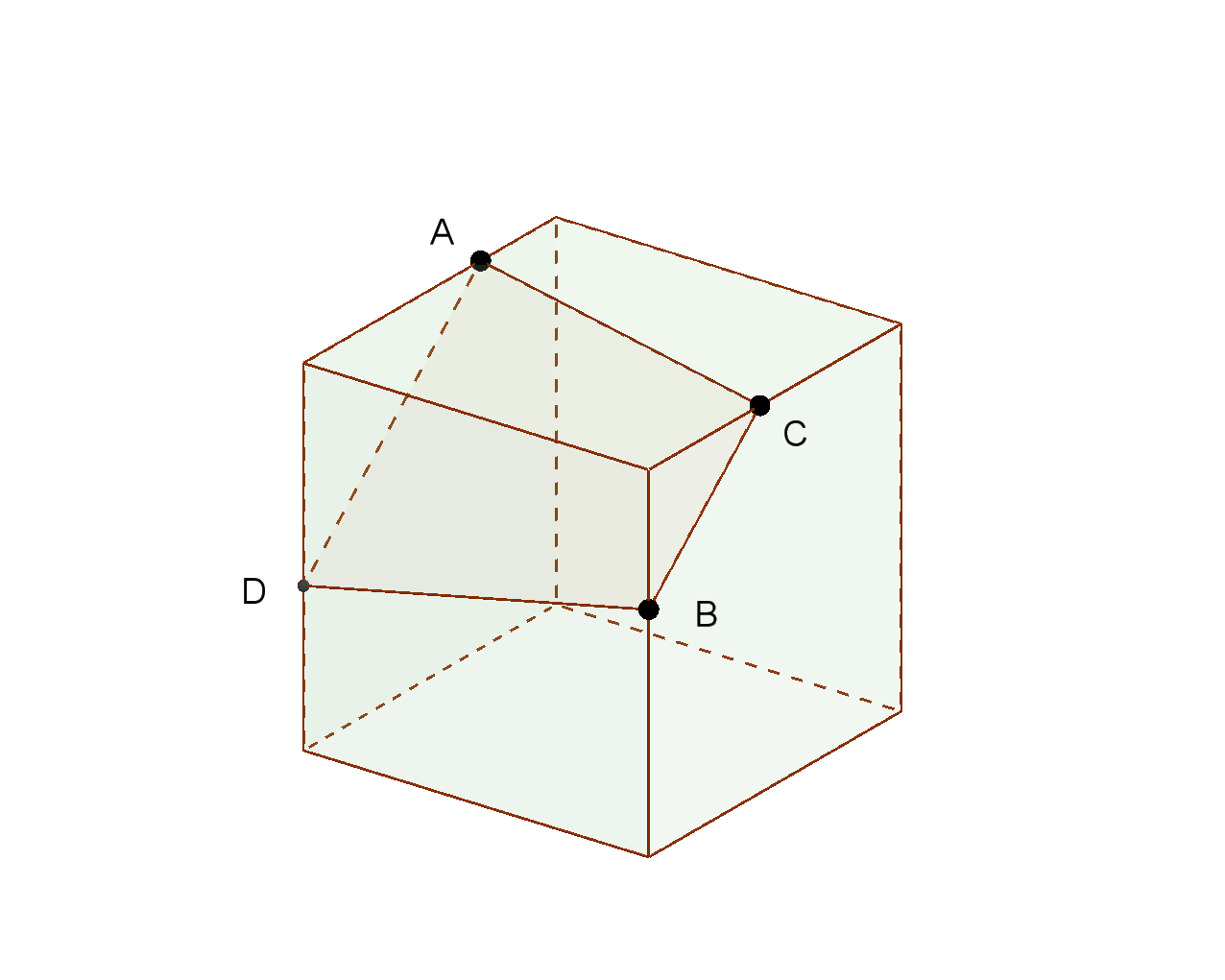
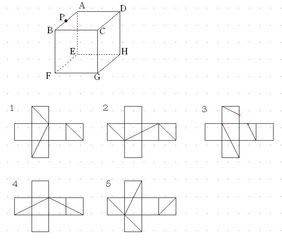
―切り口のある立方体の場合― 澤田 吉苗* 要旨 教員養成課程の女子学生を対象とした、 「生活図形科学」の授業において、読図能力を養うためのツー ルとして、切り口のある立方体の展開図を作成するソフトを開発し利用した。そのソフトは、文献1、2で 開発したソフトに、展開図を作成立方体abcdefghの辺ad、ab、cgの中点をl, m, nとする。 この立体をつぎのような平面できるとき、その切り口は何角形になるか答えなさい (1) 3点m、l、f を通る平面 (2) 3点l、m、n を通る平面 l、Mとm、fは同じ平面上にあるのでそれぞれ結べますが、そこからの作図が出来ません。この立方体を3点 A、B、C で通る平面で切った時の 切り口を書きなさい。 では、解説してゆきましょう。 まず、法則の①を使います。 同じ平面上にある点は AとCですからこの2点を結びます。 ここまでは皆さん、よくできると思います。 しかし、この後、どうしていいか 図とにらめっこの生徒さんが多いのではないでしょうか。 点AとCは結べたけれども、点Bを




中1 20 5 立方体の切断と体積 Youtube



立体の切断 中学受験ブログ
回転体 立方体の切り口 円錐の側面積 正多面体 正四面体→正八面体+4正四面体 正四面体←→正四面体 立方体→正四面体+4三角錐 立方体と正八面体 立方体←→正八面体 その2 弧の長さ・面積 転がる正方形平面切り口グラフ 切り口グラフを数えれば, 展開図の個数を数えることができます。 しかし, 3次元空間内の図形を考えるのは難しいです。 そこで, 立方体グラフを1つの頂点で切り離し, 平面上に広げま す。図3の図全体を平面立方体グラフ, 赤の辺と頂点から成る図



三石 数学塾 立方体の切り口 その1




立体切断 その4 中学受験算数の家庭学習教材 カンガループリント



3



Newみんなの算数講座56 何個壊れて何個無事 中学受験の算数知恵宝庫




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり
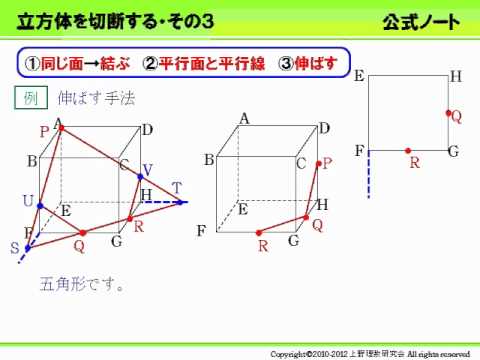



立方体の切断2 Youtube



よく見かけますね この展開図 後編 中学受験プロ講師ブログ



立体切断の3つの基本 中学受験プロ講師ブログ



空間図形 立方体の切断面を作図する 切り口の多角形はどんな形 ページ 2 みみずく戦略室



立方体の切断の問題です 切り口を台形にするには どうやって線を引けば Yahoo 知恵袋



Newみんなの算数講座66 切り口のレジュメ 後編 中学受験の算数知恵宝庫



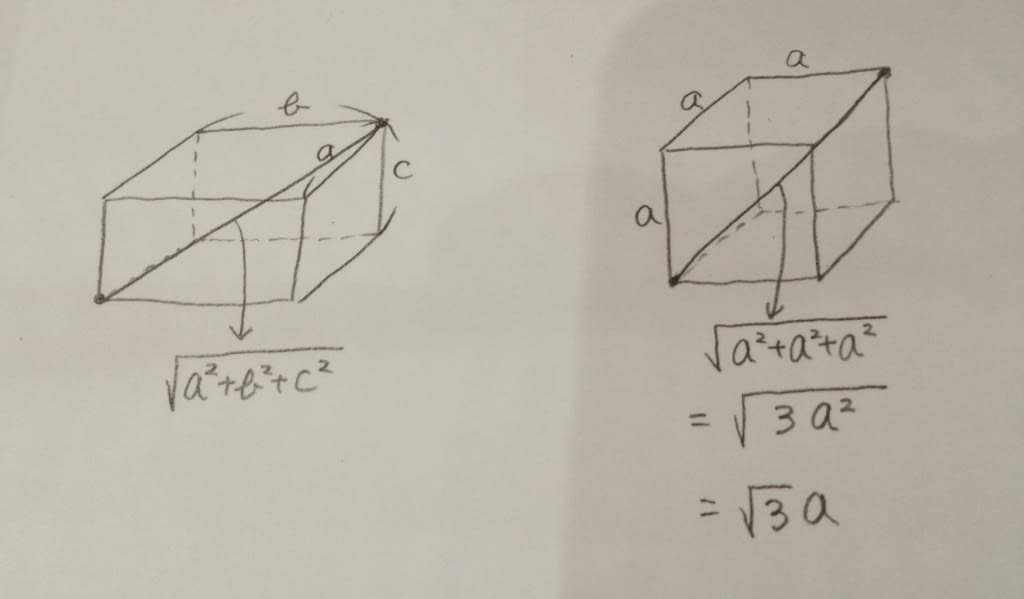
立方体の切断面の頂点からの距離 中学数学の無料オンライン学習サイトchu Su




Nl Ab Ad B Mi A N D Descubre Como Resolverlo En Qanda




メルカリ 立方体切断図形b 5パターン 参考書 1 480 中古や未使用のフリマ



空間図形 立方体の切断面を作図する 切り口の多角形はどんな形 ページ 4 みみずく戦略室




立方体の切断の攻略 受験脳を作る 村上綾一 村上綾一 本 通販 Amazon




レベル別解説 レベル選択アドバイス 中高一貫コース 通信教育 中学生 中学生 z会




立方体の切断の攻略 受験脳を作る 村上綾一 村上綾一 本 通販 Amazon




問題174 立方体に潜む正多角形




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




頭大丈夫 と心配されるシグマゼミ 立方体の切断面を描けない子が多い っていうツイートが流れてきたけど そもそも中学で 同じ平面上の点はそのまま結べる 平行な面には平行な切り口 っていう原則の部分をきちんと扱ってないんでないかなぁ あ



立方体を次の平面で切るとき切り口はどんな図形か 1 3点b D Hを通 Yahoo 知恵袋




切断面のある立体の表面積 算数の問題 身勝手な主張



Http Www Sakane Net Suugaku 3zukei 32kuukanzukei 3251setudan Rippoutai Pdf




立方体の切り口の形は 3点を通る平面はただ1つに決まります Ppt Download



1



図の立方体abcd Efghを1つの平面で切ると 切り口の図形は多 Yahoo 知恵袋



講義内容3



Q Tbn And9gcrj00x2vkwuiczuiwmdp9q7uhemucvgmdfgy5agi Qiasobhy X Usqp Cau



立方体の切断面 Geogebra




立体の切断が面白いほどできる 究極の立体切断 アプリ 現役塾講師の合格応援サイト




立方体の切断 に関するまとめをアップしました お見逃しなく 恋する中高一貫校 適性検査 徹底攻略
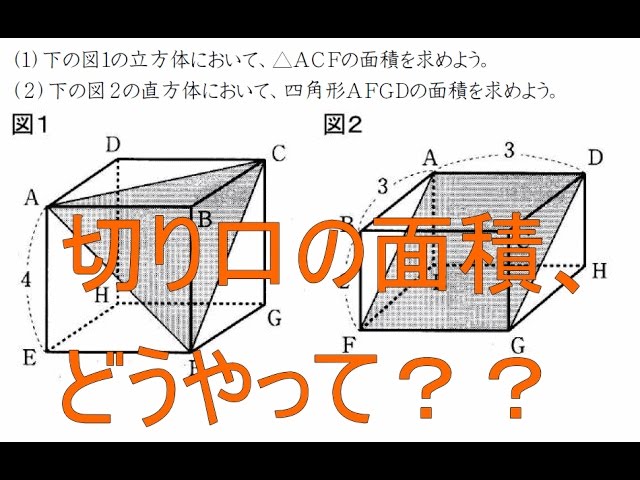



立体の切り口の面積 中学3年数学 Youtube



My Math Note




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり



空間図形 立方体を切断したときの切り口の考え方 中学数学 定期テスト対策サイト



この一題 解説編 灘 H25第2日 5 ナキイルカは ブログを はじめた



よく見かけますね この展開図 後編 中学受験プロ講師ブログ



算数限界編の解答



楽天ブックス 立方体の切断の攻略 本
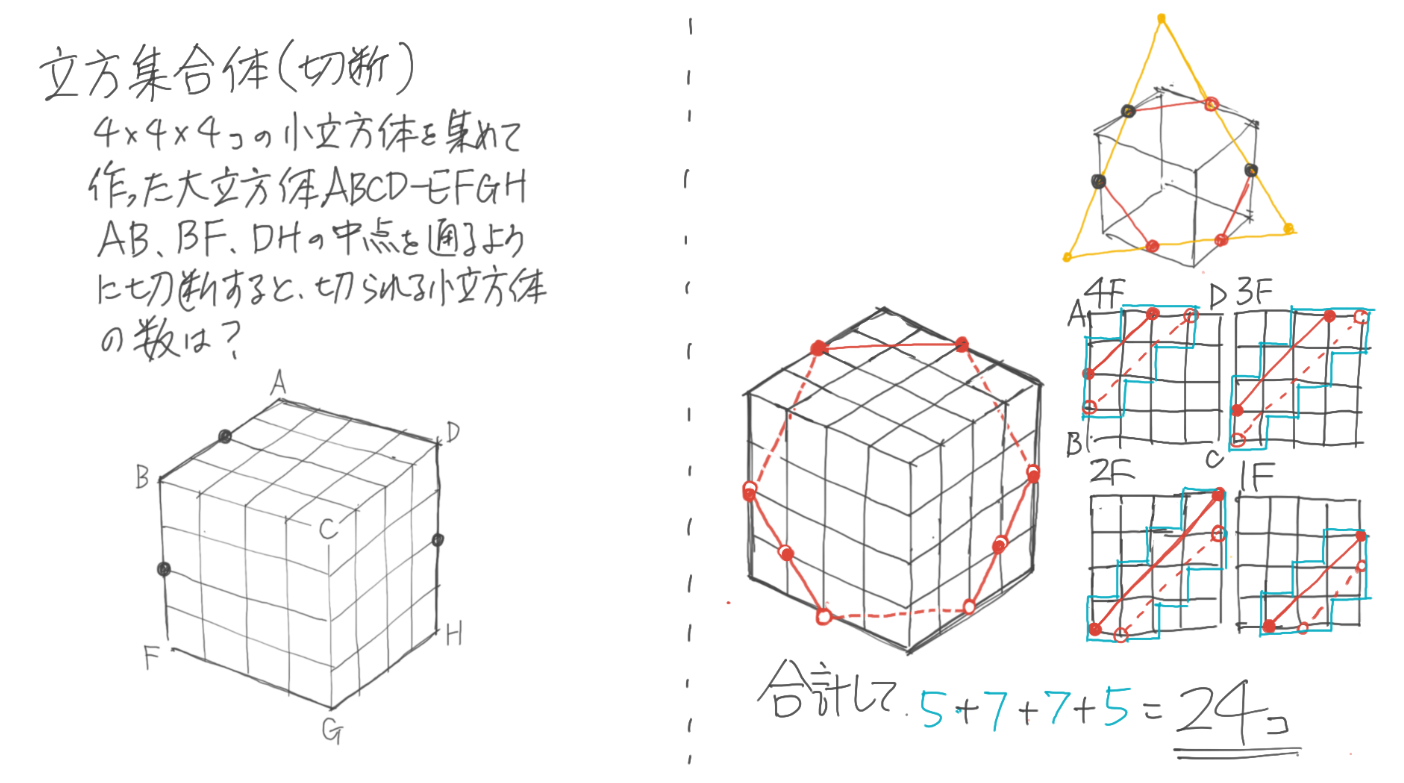



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ




立方体の個数について 同じ大きさの立方体を125個積み上げて図のような大 Okwave
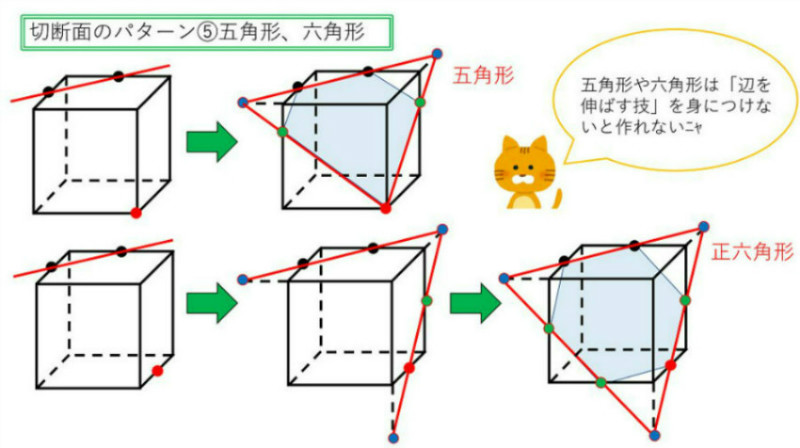



講義内容3
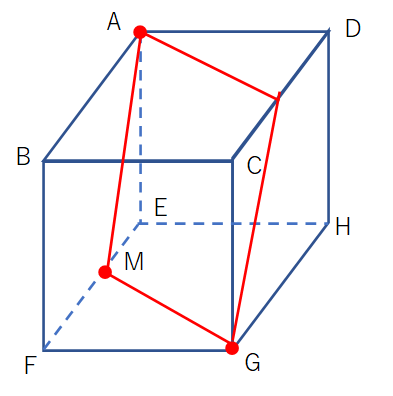



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ



たんけん立方体 塾 幼児教材 パズル教材 エジソンクラブ 法人向け販売



立体切断の考え方 中学受験 田中貴 Com



立方体の切り口 御三家中学受験 桜蔭 開成 東大サピックス家庭教師 ファインウェブ 楽天ブログ



すぐるゼミ 立体の切断1



Math 空間図形 立体の切断と切り口 働きアリ The 2nd




立方体の切り口の問題 中学受験塾の6年生レベル これを小学生低学年クラスで教えます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




立方体の切断の問題 16年本郷中 元オカマの家庭教師の独り言



ガスコン研究所



立方体の切断 19年度奈良県教員採用試験小学全科9 公務員試験知能 教員採用試験数学解説




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




立方体切断 13パターン 分数パズルの通販 By ゆうまり Shop ラクマ




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




立方体の切断面を考えてみよう Geogebra



切断面 数学mass Math



みんなの算数講座 第56講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん




問題174 立方体に潜む正多角形



立方体の切断 慶應義塾中等部 受験算数問題 00年 どう解く 中学受験算数




ウチダ 教材総合カタログ 中学校



中学数学 空間図形 立体の切断問題のコツ



My Math Note



立方体の切り口はどんな図形 1 0 Android Apk Free Download Apkturbo




立方体の切り口 Geogebra



晃華学園10 6 立体図形 立方体を平面で複数回切断する 気まぐれ解説カフェ 仮



立方体 切断 展開図 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



5 12 立体の切り口を求めるには さんすうがく



立体切断の3つの基本 中学受験プロ講師ブログ




たんけん立方体 塾 幼児教材 パズル教材 エジソンクラブ 法人向け販売



切断 立体図形 その2 前田昌宏の中学受験が楽しくなる算数塾



立方体の切断面 3つのポイントを使えば 切り口の図形が分かる バカでもわかる 中学数学



立体 立方体 の切断の問題一覧 中学受験の算数 理科ヘクトパスカル




メルカリ 立方体切断a 5パターン 参考書 1 480 中古や未使用のフリマ



1 2 Descubre Como Resolverlo En Qanda



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Vb Samples 001 2b Rippoutai Setsudanmen001 Pdf



楽天ブックス 立方体の切断の攻略 本




立方体の切断 基本の切断 駒澤塾 中学受験の算数 理科




中学受験算数教材 立方体の切断 アキラショップ
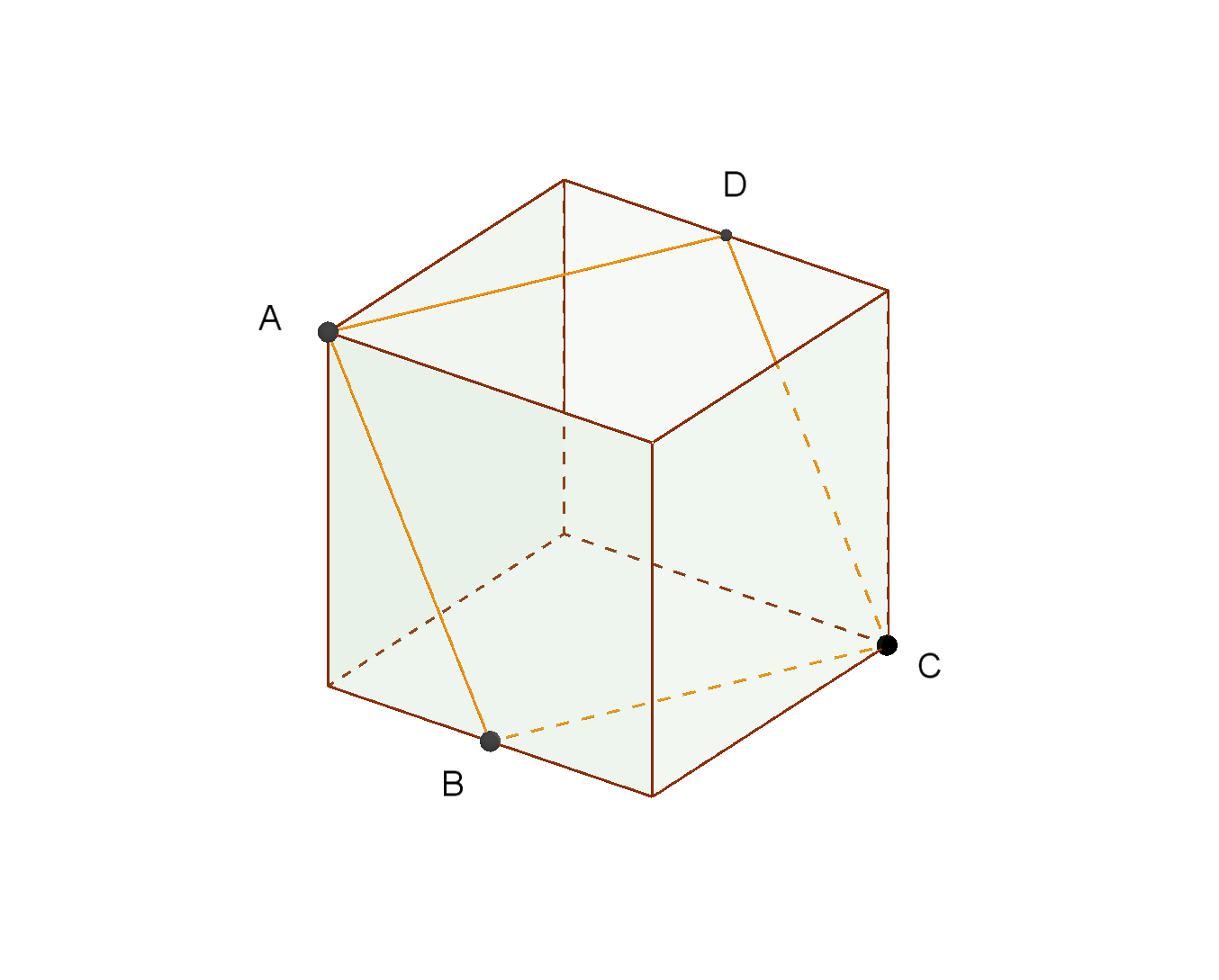



My Math Note




立方体の切断 中学受験準備のための学習ドリル




立方体の切断面 問題集の解説 Youtube
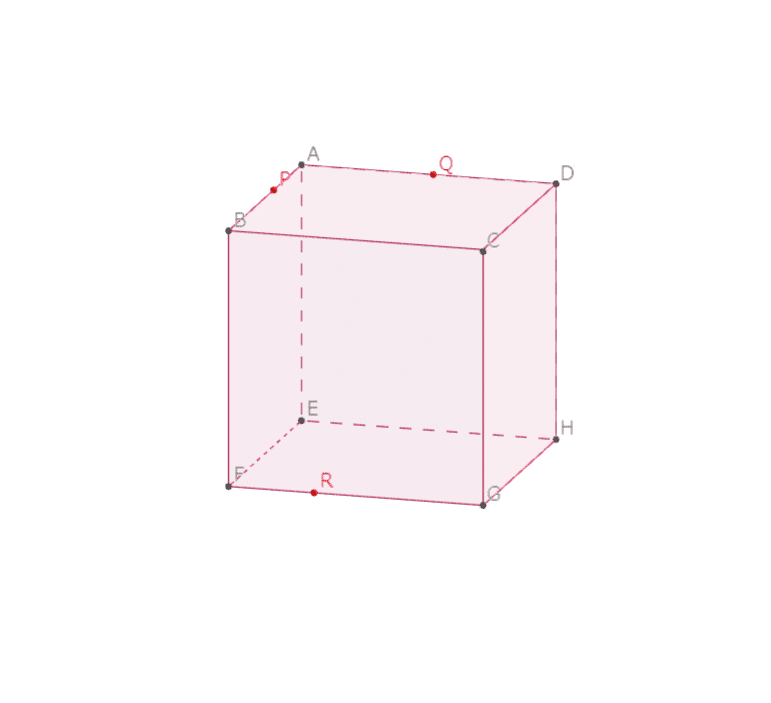



立方体の切断 切断箇所の位置や立体の体積を求める場合 直角三角形や三角錐の相似に注目する 立方体の切断で切り口 が正六角形になるとき 切断されてできた立体は同じ形になる ワンセンテンス算数 Note



立方体の切り口のイメージを見る 算数解法の極意
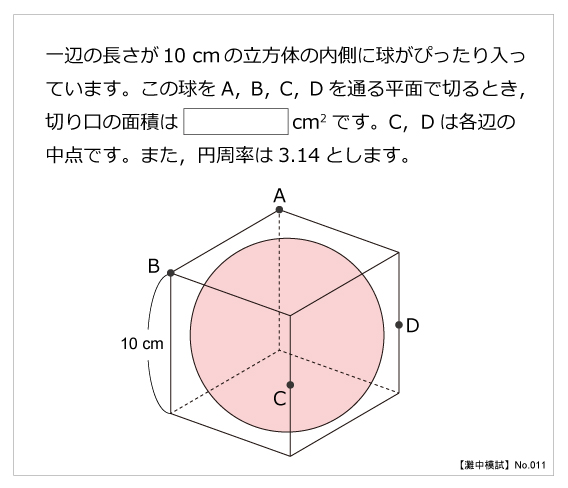



灘中模試 No 011 立体図形 算数星人のweb問題集 中学受験算数の問題に挑戦




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり



3



立方体の切断と体積 東邦大学付属東邦中学 2017 どう解く 中学受験算数




立方体 小立方体の切断 の問題 中学受験の算数 理科ヘクトパスカル


コメント
コメントを投稿